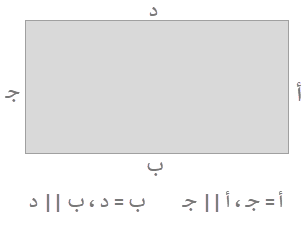المستطيل هو احد الاشكال الهندسية (مثل: المربع والدائرة و المثلث .. الخ). وخواصه هي التي تحدد اذا كان الشكل الذي لدينا هو مستطيل ام لا. فمن اشهر خواص المستطيل هي أضلاعه الأربعة .. وزواياه القائمة. ليس ذلك فقط بل توجد خواص اخرى مهمة للمستطيل ..
ما هي خواص المستطيل ؟
للمستطيل اضلاع واقطار و زوايا ، وهذه العناصر هي التي تشكل لنا المستطيل وتحدد لنا ايضاً خواصه.
اضلاع المستطيل
من خواص المستطيل هو انه يتكون من 4 اضلاع. وكل ضلعين متقابلين به متوازيان وايضاً متساويا في الطول. كما موضح في الصورة التالية:
ننتقل بعد ذلك الى اقطار المستطيل !
أقطار المستطيل
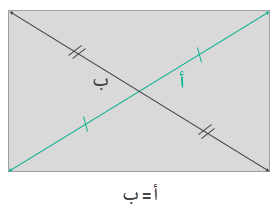
يتكون المستطيل من قطران، وهم متساويين في الطول. ومتقاطعين بحيث ينصف كل منهما الأخر.
زوايا المستطيل
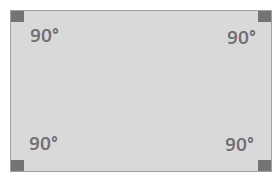
من اهم العناصر التي لانستطيع تجاهلها في تشكيل المستطيل هي زواياه. وهي من اهم الاركان التي نعتمد عليها في تحديد خواص المستطيل. حيث يتكون المستطيل من 4 زوايا وهم زوايا قائمة ، بحيث كل زواية به تساوي 90° . ومجموع زواياه تساوي 360° .
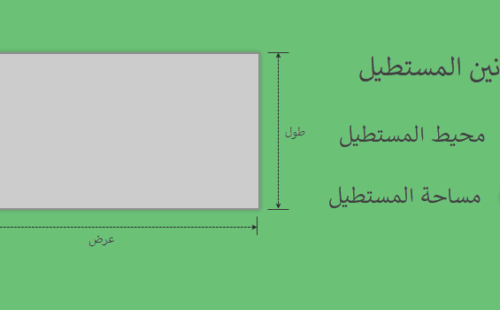
وللمستطيل ايضاً قوانين يتم استخدامها في تعيين و حساب كلاً من مساحته ومحيطه. وهذه القوانين هي تعتمد في الأساس على خواصه التي تعرفنا عليها.
قوانين المستطيل
سوف اتكلم معك بإجاز ، لاني شرحت من قبل قوانين المستطيل بالتفصيل وبالامثلة العملية في هذا الموضوع هنا . ولكن دعنا نلقي نظرة سريعة.
ابدأ معك في البداية بقانون محيط المستطيل، فبديهياً يمكننا حساب محيط المستطيل من خلال جمع اضلاعه الاربعة، وبما ان لدينا معلومة تقول بان كل ضلعين متقابلين في المستطيل متساويين فإنه يمكننا حساب محيط المستطيل كل التالي:
على سبيل المثال: لو لدينا محيط طوله 4 سم و عرضه 7 سم، فانه يمكننا حساب محيطه كالتالي:
الحال:
محيط المستطيل = ( 4 + 7 ) × 2
= ( 11 ) × 2
= 22 سم
وبالنسبة لمساحة المستطيل فإنه يمكننا تعينها من خلال ضرب طول المستطيل في عرضه.
مساحة المستطيل = الطول × العرض
دعنا نطبق قانون المساحة على المثال السابق ،
مساحة المستطيل = 4 × 7
= 28 سم2
في النهاية انصحك بإلقاء نظرة على موضوع قوانين المستطيل من هنا لإحتواءه على المزيد من شروحات العملية في حسابات المستطيل. وسوف تجد ايضا ً به المزيد من الامثلة المتقدمة الغير مباشرة في حساب كلاً من مساحة ومحيط المستطيل.