المثلث قائم الزاوية هو احد انواع المثلثات ، وهو سمي بهذا الاسم لأن أحد زواياه تساوي 90 درجة. واليوم سوف نتكلم عن بعض خواصه وقانون كلاً من المساحة والمحيط الخاصة به، مع حل بعض الأمثلة عليه.
وفي البداية سوف ابدأ معك سريعاً بالتعرف على بعض خواص المثلث القائم،..
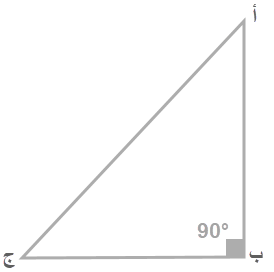
خواص المثلث قائم الزاوية
من أهم خصائص المثلث القائم:
- احد زواياه تساوي 90 درجة ، و مجموع الزاويتين الأخيرتين يساوي 90 درجة.
- المثلث القائم يحقق ويخضع لنظرية فيثاغورس.
- الضلع ع هو وتر المثلث.
- للمثلث القائم ثلاثة ارتفاعات، اثنان منهما يمثلان أحد ضلعيه، وهما الذي يشكلان الزاوية القائمة ، أما الارتفاع الثالث فهو الخط المستقيم الساقط من الزاوية القائمة على الوتر.
انتقل بك بعد ذلك… الى طرق حساب مساحة المثلث القائم،…
مساحة المثلث القائم
يمكنك حساب مساحة المثلث قائم الزاوية باستخدام القانون العام لمساحة المثلث وهو:
مساحة المثلث = نصف القاعدة × الارتفاع
مثال 1
مثلث طول قاعدته 7 سم وارتفاعه 10 سم ، احسب مساحته.
الحل:
مساحة المثلث = 3.5 سم × 10 سم
= 35 سم 2
مثال 2
مثلث طول قاعدته 10 سم وارتفاعه 13 سم ، فما هي مساحته ؟
الحل:
مساحة المثلث = 5 سم × 13 سم
= 65 سم 2
انتقل بك بعد ذلك الى طرق حساب محيط المثلث قائم الزاوية ، و سوف نتعرف على عدة طرق لذلك..
محيط المثلث القائم
ويمكن حساب محيط المثلث القائم بعدة طرق أولها القانون:
محيط المثلث = مجموع اطول اضلاعه
مثال 3
مثلث اطوال اضلاعه هي 5 سم ، 7 سم ، 10 سم احسب محيطه
الحل:
محيط المثلث = 5 سم + 7 سم + 10 سم
= 22 سم
مثال 4
مثلث أطوال اضلاعه هي 7 سم ، 10 سم ، 15 سم. قم بحساب محيطه
الحل:
محيط المثلث = 7 سم + 10 سم + 15 سم
= 32 سم
وتوجد بعض الامثلة المتقدمة في حساب محيط المثلث القائم ، مثل الأمثلة التي المتعلقة بنظرية فيثاغورس ، وتقدر تشاهدها على هذا الرابط
لمزيد من الاستفسارات تواصل معي من خلال التعليقات بالاسفل. وايضاً قم بحل التمرين التالي للتأكد من فهم لموضوعنا اليوم.
تمرين
مثلث نصف قاعدته يساوي 4.5 سم و ارتفاعه يساوي 8.5 سم ، احسب مساحته. (حل التمرين واترك حله في تعليق بالاسفل)
مواضيع اخرى متعلقة
- حساب مساحة المثلث متساوي الساقين
- مساحة المثلث متساوي الأضلاع ، طرق حسابه بالأمثلة
- ارتفاع المثلث ؟ وطرق حساباته ؟
- قوانين المثلث: مساحة ومحيط المثلث – مع الشرح بالأمثلة
- محيط المثلث متساوي الساقين ؟ وحساب قوانينه
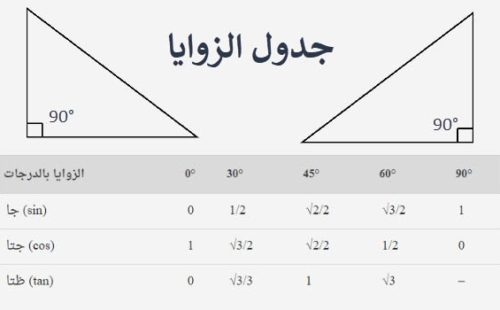
- جدول الزوايا


سلام عليكم نشكركم علي تفاعلكم