حينما نسير في الشارع ونحن ذاهبين إلى العمل، أو إلى الجامعة، نجد المباني الشاهقة، والكباري العملاقة تحيط بنا من كلّ جانب، فعندما ننظر إلى تلك المنشآت فنحن في حقيقة الأمر ننظر إلى سجلٍّ حافلٍ من جهود علماء الرياضيّات، من الجبر، والهندسة، وحساب المثلّثات، فلولا جهود هؤلاء لظلّ الإنسان يقبع في الأبنية البدائيّة حتّى يومنا هذا، ولكنّ هؤلاء العلماء العظام جعلوا لنا العالم من حولنا عالمًا رقميًّا بمعنى الكلمة، وحساب المثلّثات وما يعتمد عليه من علاقات الزوايا والأضلاع ليس ببعيدٍ من هذا، وجدول الزوايا من الأشياء الهامّة في هذا العلم الواسع، فتعالوا بنا نتعرّف عليه من خلال مقالنا هذا، فتابعونا.
جدول الزوايا
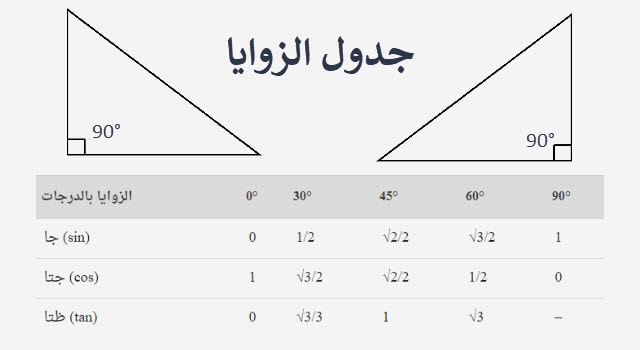
جدول الزوايا هو عبارة عن جدول يحتوي على حساب علاقة الزوايا الخاصّة في المثلّث قائم الزاوية، وهي الزوايا صفر، °30، °45، °60، °90، بأطوال الضلعين الآخرين المقابلين لهما بالوتر، ولكي نتعرّف على جدول الزوايا، سوف نتناول باختصار نظريّة فيثاغورس، ثمّ العلاقات الهندسيّة الواردة بالجدول، ثمّ نتناول مكوّناته بالتفصيل، وذلك على النحو التالي:
| الزوايا بالدرجات | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| جا (sin) | 0 | 1/2 | √2/2 | √3/2 | 1 |
| جتا (cos) | 1 | √3/2 | √2/2 | 1/2 | 0 |
| ظتا (tan) | 0 | √3/3 | 1 | √3 | – |
ماهيّة المثلّث
تتعدّد الأشكال الهندسيّة ما بين الدائرة، والمربّع، والمستطيل، وغيره، وبطبيعة الحال المثلّث، ومن خلال الاسم نستطيع أن نُعرّف المثلّث بأنّه عبارة عن: “شكل هندسيّ مغلق، مكوّن من ثلاثة أضلاع متناسبة الأطوال، يحصر كلّ ضلعين متجاورين عند نقطة إلتقائهما زاوية، تتناسب مع الضلع المقابل لها، ومجموع تلك الزوايا مائة وثمانون درجة”.
علاقة زوايا المثلّث بالأضلاع المقابلة لها
استطاع العلماء أمثال فيثاغورس، وغيره من علماء الهندسة أن يكتشفوا أنّ هناك علاقةً رياضيّةً بين الزاوية في المثلّث والضلع المقابل، ويمكن إيضاحها في الآتي:
* بفرض أنّ المثلّث قائم الزاوية، وأيضًا مع ملاحظة أنّ أي مثلّث لا يحتوي إلّا على زاوية قائمة واحدة، والتي قياسها يساوي °90، فإنّ:
- الضلع المقابل للزاوية القائمة هو أطول أضلاع المثلّث.
- كلّما زاد قياس الزاوية زاد قياس الضلع المقابل لها.
- أيّ زيادة في أحد أضلاع المثلّث يتبعه نقص متناسب مع تلك الزيادة في الضلع الثاني، مع افتراض ثبات طول الوتر- الضلع المقابل للزاوية القائمة-
- الضلعان المقابلان لزاويتين متساويتين متساويان، وبالمقابل فإنّ الزاويتين المقابلتين لضلعين متساويين متساويتان.
- مجموع أيّ ضلعين في المثلّث أكبر من الضلع الثالث.
- ضلع الزاوية المطلوبة المحصورة مع الوتر يسمّى المجاور، والضلع المقابل لها يسمّى المقابل.
نظريّة فيثاغورس
تناولت نظريّة فيثاغورس إيجاد طول الضلع المقابل للزاوية القائمة في المثلّث بمعلوميّة الضلعين الآخرين، ونصّها: “في المثلّث القائم الزاوية مساحة سطح المربّع المُنشأ على الوتر يساوي مجموع مساحتيّ سطحيّ المربّعين المُنشأين على الضلعين الآخرين”.
العلاقات الهندسيّة الواردة بجدول الزوايا هي:
- جا الزاوية sin x: يساوي طول الضلع المقابل للزاوية x على طول الوتر.
- جتا الزاوية cos x: يساوي طول الضلع المجاور للزاوية x على طول الوتر.
- ظلّ الزاوية tan x: يساوي طول الضلع المقابل للزاوية x على طول الضلع المجاور لها.
تكوين جدول الزوايا
يتكوّن جدول الزوايا من أربع حالات في المثلث قائم الزاوية، الحالة الأولى عندما يكون قياس زاويتي المثلّث يساوي °45، والحالة الثانية عندما يكون قياس الزاويتين °30، °60، والثالثة عندما يكون قياسهما يساوي صفرًا، والرابعة للزاوية القائمة ذاتها، ومن جميع ما تمّ تناوله سابقًا يمكننا تكوين جدول الزوايا كالآتي:
الحالة الأولى:
إذا كان لدينا مثلّث قائم الزاوية في y، وبه زاوية قياسها °45، فإنّ نسب أطوال أضلاعه تساوي : √2 : 1 : 1، من نظرية فيثاغورس، ومنه جيب الزوايا يساوي:
1. جا °45 sin يساوي 2√/2
2. جتا °45 cos تساوي 2√/2
لماذا…..؟ اكتشف السبب…. لأنّ المقابل والمجاور متساويان.
3. ظا °45 tan تساوي sin x / cos x .
الحالة الثانية:
عندما تكون زاويتا المثلث °30، °60، فإنّ نسب أطوال أضلاع المثلّث تساوي 1: 2 :3 √وذلك من نظريّة فيثاغورس، وجيب الزوايا يساوي:
- جا sin 30° تساوي √1 / 2، وجا sin 60° تساوي 3√ /2 .
- جتا °30 cos تساوي جذر3/ 2، وجتا cos 60° تساوي جذر 1 /2
- ظا tan تساوي sin x / cos x.
الحالة الثالثة:
- عندما يكون قياس الزاوية صفرًا فإنّ:
- جا °0 sin تساوي صفرًا؛ لأنّ المقابل يساوي صفرًا، وجتا °0 cos تساوي 1؛ لأنّ المجاور يساوي الوتر.
- ظا °0 tan تساوي صفرًا؛ لأنّ المقابل يساوي صفرًا.
الحالة الرابعة:
عندما تكون الزاوية تساوي °90 فأنّ:
- جا °90 sin تساوي 1؛ لأنّ المقابل هو ذاته الوتر.
- جتا °90 cos تساوي صفرًا؛ لأنّ المجاور لها يساوي صفرًا.
- ظا °90 tan قيمة غير معرّفة؛ لأنّها تساوي المقابل/ المجاور، والمجاور يساوي صفرًا.
* مع ملاحظة أنّه يمكن تغيير أبعاد المثلّث، مع مراعاة التقيّد بنظريّة فيثاغورس، ولكن مع ذلك ستظلّ النسب بين أضلاع المثلّث قائمة كما هي؛ لأنّها تتغيّر بنسب متساوية.
اقرا أيضا
يعدّ حساب المثلثات من العلوم النظريّة والتطبيقيّة في آنٍ واحد، وجدول الزوايا جدولٌ لانهائيّ الزوايا؛ ولذا يتمّ الاستعانة بجدول الزوايا الخاصّة في إيجاد علاقات الزوايا الأخرى، وربما تُكتشف في المستقبل علاقاتٌ أخرى، تكون أكثر أهمية.

مقال رائع! جدول الزوايا والنسب المثلثية مهم جداً لفهم الرياضيات. التفسير المبسط ساعدني في استيعاب المفاهيم بشكل أفضل. شكرًا لمشاركتكم!